If you’ve ever watched Numberphile, you’ve probably heard a *lot* about prime numbers. In school prime numbers are mostly just curiosities. They’re numbers that can only be (cleanly) divided by 1 and themselves, so you hate getting them in a fraction. But the further you go in higher math, the more prime numbers seem to show up *everywhere* even in places you wouldn’t expect them.

My new favorite Numberphile video is on the reciprocals of prime numbers. A “reciprocal” of a number is just 1 divided by that number. So the reciprocal of “10” is “1/10” or in decimal form 0.1 . The video shows off the work of a 19th century mathematician named William Shanks who exhaustively catalogued the reciprocals of primes.

Because you see, prime numbers are special this way. Prime numbers don’t make “clean” reciprocals like 1/10 . The reciprocal of a prime tends to be made up of infinitely repeating digits instead. 1/7 is equal to 0.142857142857142857142857142857142857142857142857142857 with the “142857” part repeating infinitely. In math class we represented this with a line over the repeating digits. But I’m having trouble getting wordpress to properly display bars over numbers, so I’ll use “…” to represent repeating digits instead. So 1/7 would be 0.142857… in my decimal notation.

Now back to primes. What Shanks did was he took the reciprocal of larger and larger prime numbers and counted how many digits it took before the the numbers start repeating. So 1/7 repeats after 6 digits while 1/11 repeats after just 2 digits (0.09…). Shanks catalogued these repeating digits all the way up to prime numbers in the 80,000 range, whose reciprocals don’t start repeating until 60,000 digits or more.

The video is well worth a watch, and it’s fascinating to wonder if there’s any pattern to the data. But what struck me was a question from the host Brady near the beginning of the video: “do the reciprocals of all primes repeat?” The mathematician Matt Parker answered “yes” and continued the math lecture, but this got me thinking.

As soon as I told this question to a friend, they immediately said what many of you are probably thinking: “what about 1/5?” 5 is a prime number itself, but 1/5 is a nice, clean, non-repeating number of 0.2 . 2 is also a prime number and makes a clear 0.5 with its reciprocal. Maybe Matt Parker just wasn’t so attentive when he answered “yes” but it seems that not all reciprocals of primes repeat.

But then why are 2 and 5 so special? Why, out of every single prime number, are they the only ones with non-repeating reciprocals? Again I think everyone knows the answer: it has to do with Base 10, but I wanted to study this phenomenon a bit more so I did some math myself.

First, a quick note: we say our counting system is “base 10” because when writing a large number, each position in the number corresponds to units of 10 raised to some power. You may remember from school writing a number like 435 and being taught that is has “4 hundreds,” “3 tens,” and “5 ones.” AKA 435 is (4*100) + (3*10) + (5*1). It’s important that all the positions in a base 10 counting system correspond to 10^x for some value X. The hundreds place represents 10², the tens place represents 10¹, and the ones place represents 10⁰.

Now what about a base 12 counting system instead? What does the number 435 mean in base 12? Just like before, each position corresponds to some power of 12. So 12² is 144, meaning that 4 is in the “144s” place. The 3 is in the “12s” place and the 5 is still in the “1s” place because 6⁰ and 10⁰ both equal 1. So a 435 in base 6 is equal to (4*144) + (3*12) + (5*1), which would be 617 in base 10.

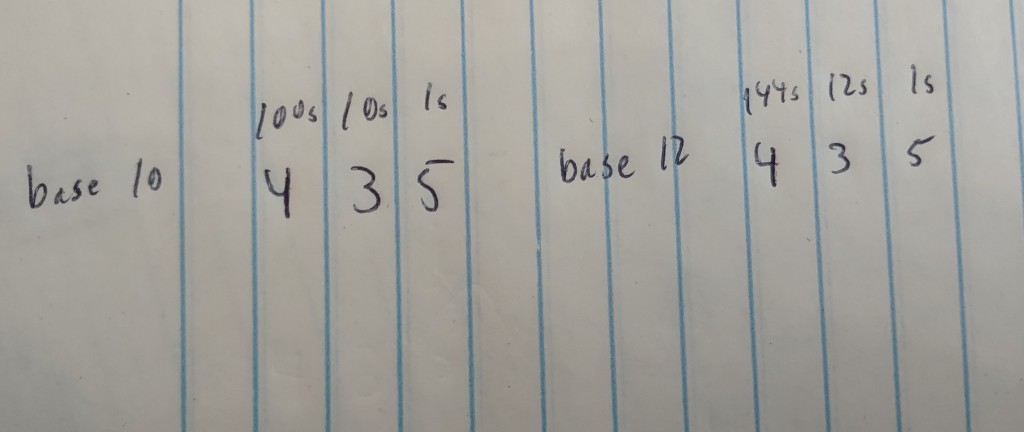
Now my question: do the reciprocals of primes still repeat the same way in a base 12 counting system as they do in base 10? We already know that 2 and 5 are special primes in base 10, their reciprocals don’t repeat. How about in base 12?

Well the reciprocal of 2 still works, it’s just equal to 0.6 instead of 0.5. But the reciprocal of 5 suddenly becomes madness

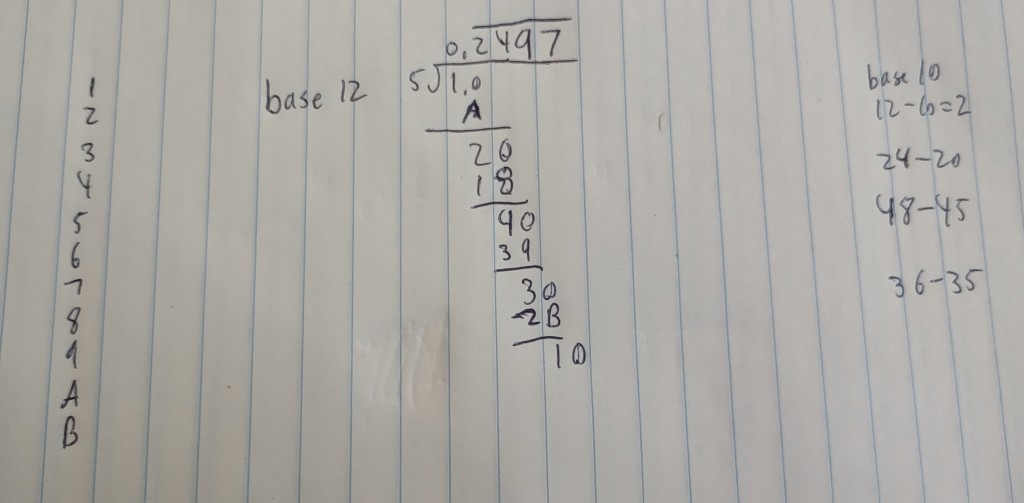
Here I did the long division for 1/5 in base 12. To keep myself on track I wrote a base-10 version of the subtractions I was doing at each step of the long division. And I don’t know how real mathematicians do it, but since I don’t have a number to represent “10” and “11” as single digits, I used “A” and “B”.

As you can see, *now* this prime’s reciprocal *does* repeat, even though it didn’t in base 10!

I think the mathematician was getting at something deeper when he said all reciprocals of primes repeat, but I’ll have to save it for another post as I had wanted to publish this one on Sunday and I’m already 3 days late.