Last time I blogged, we were dividing 1 by prime numbers using long division on a hand-written piece of paper. We saw that while 1/5 in base 10 is the simple, easy-to-remember 0.2, 1/5 in base 12 is 0.2497… with infinitely repeating digits. Why is that?

The answer I think has to do with prime factors. 10 has prime factors of 2 and 5, so in base 10 every prime number *except 2 and 5* will have infinitely repeating digits when you take its reciprocal (again, reciprocal just means “divide 1 by that number” ie the reciprocal of 5 is 1/5). When I used base 12, the reciprocal of the prime number 5 now had infinitely repeating digits, because 5 is *not* a prime factor of 12. The reciprocal of 2 in base 12 was still well-behaved, but that’s because 2 *is* a prime factor of 12.

I can generalize the above point as this: “the reciprocal of any prime number will have infinitely repeating digits, *unless* that number is a prime factor of the base you are using.”

So in base 10, the reciprocals of 2 and 5 do *not* infinitely repeat, while the reciprocal of any other prime does. In base 12, the reciprocals of 2 and *3* do not repeat, while the reciprocal of any other prime does. In base 210, the reciprocals of 2, 3, 5, and 7 do not repeat, and I can prove that because 2, 3, 5, and 7 are the prime factors of 210.

But that got me thinking, what about non-prime numbers? (For the record, mathematicians call non-primes “composite” numbers but there’s already enough jargon here so I’ll go with “non-primes”)

Do the reciprocals of non-primes repeat infinitely or do they not? Well a few examples show mixed results, 1/20 is 0.05, but 1/21 is 0.047619… with infinitely repeating 047619s. Then there are cases like 1/24, where the reciprocal starts with some non-repeating digits and then later digits repeat infinitely, 1/24 is 0.04166… with only the 6s repeating, not the 041.

It makes sense why these reciprocals all have a leading zero, when you do the long division you need to bring down more zeros before you get a number you can divide into. So the reciprocal of any number between 10 and 100 will have 1 leading zero, and between 100 and 1000 will have 2 leading zeros, etc.

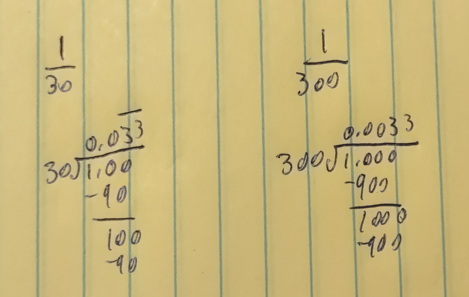
See above, the reciprocal of 30 and 300 is the same except for how many zeros you need in the front before you get to something you can divide into. (EDIT: just imaging I put the line over the 3s in 1/300, I just realized in editing that I forgot to do that, -2 points on the test for me).

But aside from leading zeros, why do some reciprocals have *only* infinitely repeating numbers and some have a set of numbers that repeat and a set of numbers that do not? I surmise again that it has to do with prime factors.

If *all* the prime factors of a non-prime number are *also* prime factors of the base you’re using (so in base 10, 2 and 5 are its factors), then the reciprocal of the non-prime number will be finite and well behaved like 1/20. On the other hand, if *all* the prime factors of a non-prime are not shared with the base (such as 21), then the reciprocal will only have repeating digits (baring leading zeros if the number is bigger than 10, 100, 1000 etc). Finally, the prime factors of a non-prime are mixed between those shared with the base and those not shared, then the reciprocal will have a bit at the beginning that does *not* repeat and will then go into repeating digits.

This should all hold true in other bases as well. In base 28, the reciprocal of 25 should be infinitely repeating (since they share no prime factors) while the reciprocal of 224 should be some non-repeating number (as 28 and 224 have the exact same prime factors, 2 and 7). I won’t show you the calculations as they’re quite messy but I think 1/224 in base 28 is 0.035 (I don’t dare do the reciprocal of 25, I’m sure to mess it up).

I’m sure mathematicians have known all this for year, but I enjoyed finding it out myself, and just wanted to share.