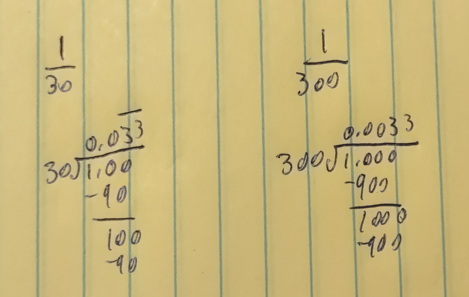Tag Archives: Math

Forecasting 101: all good trends will continue forever

This is a small addendum to yesterday’s post about forecasting.

Whenever you’re forecasting future trends, there are two general rules for the hack forecaster:

1. Every good trend will continue forever

2. Every bad trend will turn around soon

This doubly true when your forecasting has a political purpose, in which “good” and “bad” can be thought of as “supports” and “doesn’t support” your chosen narrative. A certain twitterati demonstrated this succinctly in their egg prices prediction from earlier this year:

Source

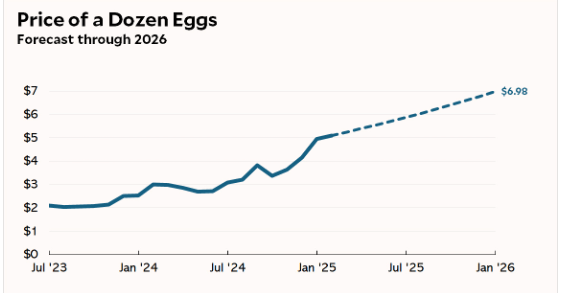
Now I don’t want to dunk too hard on this prediction (the man died between when I first saw this and when I finally got around to posting about it), but it seems like the clearest cut case of motivated reasoning I can find.  The writer was a political blogger who didn’t like the current US administration.  Saddling the administration with ever-rising prices sends a strong signal that “this administration is bad for the economy.”  So that was the prediction they wanted, and that was what they ran with.

Unfortunately for motivated reasoning, this is the chart of US egg prices since the start of the year.

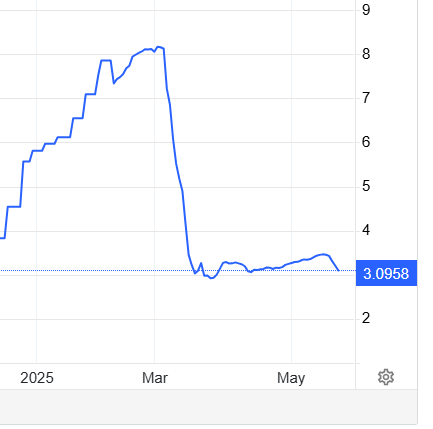
Source, that 3.0958 just rounds to $3.10 by the way

Trends don’t usually continue monotonically forever.

Why does this matter?  Well it doesn’t matter much, this is a small post.  But I wanted to make clear that forecasting is easy to do when you don’t expect accountability.  It’s the easiest thing in the world to draw a trendline continuing forever to support your narrative, and if you ever get pushback later for being wrong you can attack the complainers for “focusing on the past.”  

I think there needs to be a lot more social accountability in forecasting.  We need to stop giving a microphone to people who constantly proclaim a doom or paradise that never comes.  And our society needs to be willing to hold people accountable for their predictions. 

Back when 538 still existed and was run by Nate Silver, the thing that impressed me most about their predictions was the honesty with which they *scored* those predictions after-the-fact.  Every election cycle they looked at every race for which they made a prediction and compared the predictions to the actual outcomes.

And surprise surprise, predictions from an actual data scientist were quite accurate.  People hate on Nate Silver for predicting Trump had a 30% chance of winning in 2016 (instead of 100%, since he *did* win, or 0% since so many people claimed he could *never* win).  But true to form, any event that 538 gave a 30% chance to had about a 30% chance of happening.  Over the hundreds of elections that they predicted, they gave out a lot of 30% chances, and yes those 30% events did happen 30% of the time. They didn’t *always* happen, they didn’t *never* happen, they happened about 30% of the time.

That’s the kind of accountability we need, and its a shame that we lost it along with 538.  

More about primes

Last time I blogged, we were dividing 1 by prime numbers using long division on a hand-written piece of paper. We saw that while 1/5 in base 10 is the simple, easy-to-remember 0.2, 1/5 in base 12 is 0.2497… with infinitely repeating digits. Why is that?

The answer I think has to do with prime factors. 10 has prime factors of 2 and 5, so in base 10 every prime number *except 2 and 5* will have infinitely repeating digits when you take its reciprocal (again, reciprocal just means “divide 1 by that number” ie the reciprocal of 5 is 1/5). When I used base 12, the reciprocal of the prime number 5 now had infinitely repeating digits, because 5 is *not* a prime factor of 12. The reciprocal of 2 in base 12 was still well-behaved, but that’s because 2 *is* a prime factor of 12.

I can generalize the above point as this: “the reciprocal of any prime number will have infinitely repeating digits, *unless* that number is a prime factor of the base you are using.”

So in base 10, the reciprocals of 2 and 5 do *not* infinitely repeat, while the reciprocal of any other prime does. In base 12, the reciprocals of 2 and *3* do not repeat, while the reciprocal of any other prime does. In base 210, the reciprocals of 2, 3, 5, and 7 do not repeat, and I can prove that because 2, 3, 5, and 7 are the prime factors of 210.

But that got me thinking, what about non-prime numbers? (For the record, mathematicians call non-primes “composite” numbers but there’s already enough jargon here so I’ll go with “non-primes”)

Do the reciprocals of non-primes repeat infinitely or do they not? Well a few examples show mixed results, 1/20 is 0.05, but 1/21 is 0.047619… with infinitely repeating 047619s. Then there are cases like 1/24, where the reciprocal starts with some non-repeating digits and then later digits repeat infinitely, 1/24 is 0.04166… with only the 6s repeating, not the 041.

It makes sense why these reciprocals all have a leading zero, when you do the long division you need to bring down more zeros before you get a number you can divide into. So the reciprocal of any number between 10 and 100 will have 1 leading zero, and between 100 and 1000 will have 2 leading zeros, etc.

See above, the reciprocal of 30 and 300 is the same except for how many zeros you need in the front before you get to something you can divide into. (EDIT: just imaging I put the line over the 3s in 1/300, I just realized in editing that I forgot to do that, -2 points on the test for me).

But aside from leading zeros, why do some reciprocals have *only* infinitely repeating numbers and some have a set of numbers that repeat and a set of numbers that do not? I surmise again that it has to do with prime factors.

If *all* the prime factors of a non-prime number are *also* prime factors of the base you’re using (so in base 10, 2 and 5 are its factors), then the reciprocal of the non-prime number will be finite and well behaved like 1/20. On the other hand, if *all* the prime factors of a non-prime are not shared with the base (such as 21), then the reciprocal will only have repeating digits (baring leading zeros if the number is bigger than 10, 100, 1000 etc). Finally, the prime factors of a non-prime are mixed between those shared with the base and those not shared, then the reciprocal will have a bit at the beginning that does *not* repeat and will then go into repeating digits.

This should all hold true in other bases as well. In base 28, the reciprocal of 25 should be infinitely repeating (since they share no prime factors) while the reciprocal of 224 should be some non-repeating number (as 28 and 224 have the exact same prime factors, 2 and 7). I won’t show you the calculations as they’re quite messy but I think 1/224 in base 28 is 0.035 (I don’t dare do the reciprocal of 25, I’m sure to mess it up).

I’m sure mathematicians have known all this for year, but I enjoyed finding it out myself, and just wanted to share.

What’s so special about prime numbers?

If you’ve ever watched Numberphile, you’ve probably heard a *lot* about prime numbers. In school prime numbers are mostly just curiosities. They’re numbers that can only be (cleanly) divided by 1 and themselves, so you hate getting them in a fraction. But the further you go in higher math, the more prime numbers seem to show up *everywhere* even in places you wouldn’t expect them.

My new favorite Numberphile video is on the reciprocals of prime numbers. A “reciprocal” of a number is just 1 divided by that number. So the reciprocal of “10” is “1/10” or in decimal form 0.1 . The video shows off the work of a 19th century mathematician named William Shanks who exhaustively catalogued the reciprocals of primes.

Because you see, prime numbers are special this way. Prime numbers don’t make “clean” reciprocals like 1/10 . The reciprocal of a prime tends to be made up of infinitely repeating digits instead. 1/7 is equal to 0.142857142857142857142857142857142857142857142857142857 with the “142857” part repeating infinitely. In math class we represented this with a line over the repeating digits. But I’m having trouble getting wordpress to properly display bars over numbers, so I’ll use “…” to represent repeating digits instead. So 1/7 would be 0.142857… in my decimal notation.

Now back to primes. What Shanks did was he took the reciprocal of larger and larger prime numbers and counted how many digits it took before the the numbers start repeating. So 1/7 repeats after 6 digits while 1/11 repeats after just 2 digits (0.09…). Shanks catalogued these repeating digits all the way up to prime numbers in the 80,000 range, whose reciprocals don’t start repeating until 60,000 digits or more.

The video is well worth a watch, and it’s fascinating to wonder if there’s any pattern to the data. But what struck me was a question from the host Brady near the beginning of the video: “do the reciprocals of all primes repeat?” The mathematician Matt Parker answered “yes” and continued the math lecture, but this got me thinking.

As soon as I told this question to a friend, they immediately said what many of you are probably thinking: “what about 1/5?” 5 is a prime number itself, but 1/5 is a nice, clean, non-repeating number of 0.2 . 2 is also a prime number and makes a clear 0.5 with its reciprocal. Maybe Matt Parker just wasn’t so attentive when he answered “yes” but it seems that not all reciprocals of primes repeat.

But then why are 2 and 5 so special? Why, out of every single prime number, are they the only ones with non-repeating reciprocals? Again I think everyone knows the answer: it has to do with Base 10, but I wanted to study this phenomenon a bit more so I did some math myself.

First, a quick note: we say our counting system is “base 10” because when writing a large number, each position in the number corresponds to units of 10 raised to some power. You may remember from school writing a number like 435 and being taught that is has “4 hundreds,” “3 tens,” and “5 ones.” AKA 435 is (4*100) + (3*10) + (5*1). It’s important that all the positions in a base 10 counting system correspond to 10x for some value X. The hundreds place represents 102, the tens place represents 101, and the ones place represents 100.

Now what about a base 12 counting system instead? What does the number 435 mean in base 12? Just like before, each position corresponds to some power of 12. So 122 is 144, meaning that 4 is in the “144s” place. The 3 is in the “12s” place and the 5 is still in the “1s” place because 120 and 100 both equal 1. So a 435 in base 12 is equal to (4*144) + (3*12) + (5*1), which would be 617 in base 10.

Now my question: do the reciprocals of primes still repeat the same way in a base 12 counting system as they do in base 10? We already know that 2 and 5 are special primes in base 10, their reciprocals don’t repeat. How about in base 12?

Well the reciprocal of 2 still works, it’s just equal to 0.6 instead of 0.5. But the reciprocal of 5 suddenly becomes madness

Here I did the long division for 1/5 in base 12. To keep myself on track I wrote a base-10 version of the subtractions I was doing at each step of the long division. And I don’t know how real mathematicians do it, but since I don’t have a number to represent “10” and “11” as single digits, I used “A” and “B”.

As you can see, *now* this prime’s reciprocal *does* repeat, even though it didn’t in base 10!

I think the mathematician was getting at something deeper when he said all reciprocals of primes repeat, but I’ll have to save it for another post as I had wanted to publish this one on Sunday and I’m already 3 days late.